Estudos de Platão II - The Great Ideas Program

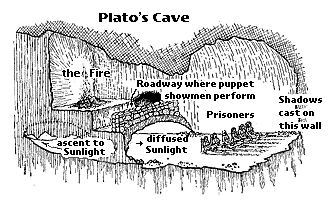
Eis a segunda leitura da República de Platão, conforme recomendada pelo The Great Ideas Program.

* * *

The Great Ideas Program – Volume 10 – Philosophy
Second Reading – Plato, The Republic, Vol 7, pp. 386d-388a, 391b-401d

Sócrates divide o mundo em dois segmentos desiguais (proporção 2:1), que por sua vez são divididos em dois segmentos também desiguais (proporção 2:1). A desigualdade espacial dos segmentos refere-se à desigualdade em qualidade, isto é, quanto maior o segmento, mais importante (maior qualidade) terá.

* * *

Sócrates convida Glauco a examinar como devem ser formados os homens com o caráter para governar o Estado.

A ginástica e as artes não são as ciências hábeis para tal uma vez que são mecânicas, isto é, lidam com o que se transforma e morre (corporal). Procuramos a ciência do essencial, não do passgeiro, efêmero, transitório.

Sócrates, então, prossegue sua investigação distinguindo objetos que não conduzem a duas sensações opostas, isto é, que não provocam a análise, dos objetos que conduzem a duas sensações opostas, isto é, que provocam a análise (ou seja, que provocam a inteligência). Expliquemos: a visão, em si, é incapaz de distinguir grandeza de pequeneza, grossura de finura etc., assim como o tato é, em si, incapaz de distinguir lisura de aspereza etc. A alma, perplexa com a vacuidade dos sentidos, ou seja, perplexa porque os sentidos dizem que algo é pequeno e grande ao mesmo tempo, faz uso do raciocínio e da inteligência para detectar se o que é visto é uma ou duas coisas. A vista, em si, é incapaz de distinguir um de dois.

O espírito, recebendo o múltiplo, é constrangido a indagar nele a unidade, pois que vemos a mesma coisa una e múltipla. Eis por que a aritmética, buscando a unidade em todos os números, até o infinito, é adequada ao filósofo para que ele alcance a essência. A aritmética tem o poder, pelo raciocínio abstrato, de levar a alma a regiões superiores, de fazer ver mais facilmente a idéia do Bem.

Similarmente, a geometria é recomendada ao filósofo, não como mera aplicação utilitária, como normalmente fazem os militares e artesãos, mas para utilizar-se das grandezas e medidas a fim de atingir suas essências. Isso se aplica também à ciência dos sólidos (modernamente chamada de “geometria espacial”), embora Sócrates e Glauco julgassem tal ciência como ainda em estágio subdesenvolvido, imprópria para os estudos filosóficos. Por extensão, a observação feita à aritmética, geometria plana e geometria espacial aplica-se também a astronomia: a lentidão/rapidez dos movimentos, por exemplo, cuja verdade deve ser apreendida pela razão e pela inteligência.

E, assim como a astronomia está ligada a visão, há uma ciência equivalente à audição: a música. O filósofo deve dedicar-se procurando números nos acordes e descobrindo quais são os números harmônicos.

O progresso ou método empregado para cada uma dessas artes, a fim de atingir o limite do inteligível, é a dialética. A dialética faz uso das artes acima para elevar a alma do homem às regiões superiores. Não há, portanto, ciência superior à dialética.

Sócrates repete as qualidades físicas e intelectuais que o protofilósofo deve possuir (ver estudo anterior). É notável que Sócrates aconselhe que as artes não devam ser ensinadas de maneira forçada pois, ao contrário do corpo cujos exercícios físicos forçados deles se aproveita, a alma rejeita a educação forçada. Sócrates prossegue, afirmando que os jovens abaixo de 30 anos de idade não devem ter muito contato com a dialética, uma vez que dela abusarão rapidamente, usando-a como um truque ou jogo.

Sócrates entende ainda que os jovens com mais de 30 anos de idade devem entregar-se à dialética pelo dobro do tempo que entregaram-se ao exercício físico, ou seja, aproximadamente 5 anos. Depois, esses jovens deverão retornar à “caverna”, exercendo funções militares durante aproximadamente 15 anos. Resumo: aos 30, o jovem dedica-se 5 anos à dialética e, aos 35, dedica-se 15 anos à funções militares e políticas. E depois dos 50 anos?

[A]nd when they have reached fifty years of age, then let those who still survive and have distinguished themselves in every action of their lives, and in every branch of knowledge, come at last to their consummation: the time has now arrived at which they must raise the eye of the soul to the universal light which lightens all things, and behold the absolute good; for that is the pattern according to which they are to order the State and the lives of individuals, and the remainder of their own lives also; making philosophy their chief pursuit, but, when their turn comes, toiling also at politics and ruling for the public good, not as though they were performing some heroic action, but simply as a matter of duty; and when they have brought up in each generation others like themselves and left them in their place to be governors of the State, then they will depart to the Islands of the Blessed and dwell there; and the city will give them public memorials and sacrifices and honor them, if the Pythian oracle consent, as demigods, but if not, as in any case blessed and divine. (pág. 401b [540]).

Sócrates lembra que o que foi dito é difícil, mas não impossível de acontecer. Basta que apenas um filósofo se torne rei. Então, as crianças com 10 anos serão separadas dos pais e educadas nos princípios desse filósofo-rei.

* * *

SELF-TESTING QUESTIONS

1. Que outro uso, além do filosófico, Platão admite para os matemáticos?

Uso militar.

2. Quais as duas razões que explicam o subdesenvolvimento das ciências matemáticas?

• Nenhum governo as patrocina.
• A dificuldade de encontrar um professor/guia.

3. Quais males o estudo da dialética introduz?

• O mal da desordem, em função das constantes refutações às quais um homem pode ser alvo, tornando-se indiferente quanto a valores como honra/desonra, honestidade/desonestidade, prudência/imprudência etc.
• O mal do ceticismo, que acomete em especial os jovens que fazem uso da dialética por diversão, refutando aqui e ali sem parar, terminando em nada acreditar.

4. Em que idade o estudante de filosofia está pronto para a visão do bem absoluto?

Aos 50 anos de idade.

5. Que operação matemática é necessária em todas as artes e ciências?

O cálculo.

6. Por que a ginástica é rejeitada enquanto educação para a filosofia?

Porque é uma ciência mecânica, que lida com aquilo que é gerado e corrompido, ou seja, que é efêmero e passageiro, e não com o essencial e imutável.

7. Quais os dois tipos de objeto de sentido, em relação ao pensamento?

• Objetos não convidativos ao pensamento, já que os sentidos bastam para julgá-los.
• Objetos intrigantes, que exigem investigação por parte do pensamento e do raciocínio.

Estudos de Platão I - The Great Ideas Program

Segue a primeira leitura da República de Platão, seguindo orientação do Volume 10 dos Great Ideas Program.

* * *

The Great Ideas Program – Volume 10 – Philosophy

First Reading – Plato, The Republic, Vol 7, pp. 369c-383a, 388a-391a

Estrutura:

1. O Estado e os filósofos
a) Por que os Estados são mal administrados?
b) Porque os filósofos não são os reis.
c) Por que os filósofos deveriam ser os reis?
d) Porque os filósofos detêm conhecimento, não mera opinião como os sofistas, sendo por isso os mais habilitados.

2. O perfil do filósofo
a) Quais as características típicas do filósofo?
b) Sinceridade, boa memória, coragem, desapego a coisas materiais e sensuais.
c) Por que os filósofos atualmente não possuem essas características?
d) Por dois motivos: (1) Os filósofos têm suas características ímpares usurpadas e desviadas desde a tenra idade e (2) O ambiente lhes é impróprio e mesmo hostil.

3. O que fazer para que um filósofo se torne rei
a) Corrigir os métodos educacionais das crianças e jovens.
b) Apresentar à multidão o verdadeiro filósofo, que logo o reconhecerá como o mais habilitado.
Como deve agir o filósofo, uma vez rei
a) O filósofo corrigirá os costumes e caracteres privados e estatais.
b) O filósofo formulará uma nova Constituição.
c) O filósofo aperfeiçoará essa Constituição, moldando as instituições de maneira que se aproximem sucessivamente do ideal.

* * *

Platão inicia fazendo Sócrates perguntar a Glauco qual a falha crucial no Estado que causa sua má administração. A resposta de Sócrates é que enquanto os filósofos não forem reis, ou os reis e príncipes não tiverem o espírito e a força da filosofia, os males da cidade não terão fim.

Glauco pede a Sócrates que se explique. Sócrates afirma que, antes, faz-se necessário descrever quem são esses filósofos a quem se deve confiar a liderança do Estado.

“[Filósofo] é aquele que tem atração por qualquer tipo de conhecimento e que está sempre curioso em aprender, nunca satisfeito”. (p. 370c)

Filosofia, etimologicamente, é amor à sabedoria. Um amante que ama algo não ama parte desse algo, mas ama o algo como um todo, por inteiro. Por exemplo, um sujeito ambicioso abraça um poder inferior quando não lhe é permitido abraçar um grande poder. Ele ama o poder, e abraça aquele que está ao seu alcance. Mas abraçará mais e mais à medida que lhe for possível.

Similarmente, o filósofo, amante da sabedoria, ama a sabedoria como um todo, e não parte dela. Embora se contente inicialmente com uma pequena porção, ele quer sempre mais e mais, já que é amante da sabedoria.

Glauco argumenta que, nesse caso, se a curiosidade dá o tom dos filósofos, então os amantes da música e das outras artes inferiores são também filósofos.

Sócrates responde que não, pois tais curiosos são, na verdade, imitações. Os verdadeiros filósofos são os amantes da visão da verdade. Os curiosos amam as belas cores e os belos sons, mas sua inteligência é incapaz de ver ou amar a beleza absoluta.

Ora, se a sabedoria está relacionada ao ser (já que saber é saber algo) e a ignorância está relacionada ao não-ser (já que ignorar é nada saber), há um meio-termo entre eles. É o âmbito da opinião, ou seja, o âmbito daqueles que enxergam as coisas belas mas não vêem a beleza, que enxergam a justiça nas ações mas são incapazes de ver a essência da justiça.

As opiniões são relativas, dependem do ponto de vista, da posição, do dia, da pessoa. Algo belo de certo ponto de vista poderá ser feio sob outro ponto de vista. O dobro pode ser metade. Glauco lembra-se então dos enigmas em forma de trocadilho, nos quais algo parece ser uma coisa mas também pode ser outra, ambiguamente, como as opiniões.

Sócrates e Glauco concordam, então, que o filósofo é o mais habilitado ao comando do Estado, a não ser que alguma virtude ou experiência lhe falte em relação aos amantes da opinião.

Sócrates passa então a enumerar diversas qualidades que os filósofos, por natureza, devem possuir: sinceridade, desapego a prazeres corporais, temperança, coragem (pois não temem a morte), prazer em aprender, boa memória; em suma, uma mente de conformação graciosa e proporcional.

Adimanto, porém, discorda de Sócrates, lembrando que os filósofos em geral não possuem tais qualidades, sendo bem o contrário: são rudes, inúteis, “monstros estranhos”.

Ora, Sócrates concorda, mas não que os filósofos sejam inúteis em si, mas que tenham sido tornados inúteis pelos que os cercam. E quanto às corrupções de caráter (rudes etc.), Sócrates compara o filósofo a uma semente vigorosa: se plantada em bom solo, bons frutos dará; se plantada em mau solo, péssimos frutos dará. O grande potencial de um filósofo, em meio a um ambiente hostil e refratário, renderá grandemente negativo, salvo por intervenção divina.

Sócrates continua, acrescentando que os sofistas são meros professores das opiniões alheias, capazes de descrever seus gostos e temperamentos mas incapazes de inferir delas o que é absoluto e imutável.

Além disso, desde a tenra idade, aquele que tem potencial para a filosofia terá seus talentos usurpados pelos seus concidadãos. Assim, bajulado e desviado, o protofilósofo não se submeterá à razão, torpe que está. Mesmo que porventura o protofilósofo acorde da ilusão em que vive, ainda assim seus concidadãos e amigos tentarão convencê-lo a largar a filosofia para que não percam as vantagens que desfrutam de sua usurpação, nem que para isso o leve aos tribunais. É quase impossível, portanto, que os filósofos prosperem num ambiente assim.

A filosofia acaba sendo ocupada, então, por medíocres e imitadores, que, encantados com títulos e pompas, a deturpam e denigrem. Sócrates compara tal desgraça com um ferreiro baixo e calvo (o medíocre) que, bem arrumado e bem vestido, casa-se com a filha do patrão, reduzindo-a a miséria (a filosofia rebaixada).

Após tal processo de filtragem, tem-se que o número de filósofos será baixíssimo. Essa diminuta classe poderia se dar por contente caso mantenha-se à margem das multidões, desfrutando das bênçãos da filosofia. Mas, ao mesmo tempo, o filósofo sabe que seu desempenho teria sido máximo se o Estado fosse o mais adequado para o desenvolvimento de seus talentos.

Sócrates passa então a discorrer como o Estado deve agir na educação de jovens e crianças para que a filosofia não pereça. O Estado não deve sobrecarregar as crianças e jovens com muita filosofia, mas sim com mais ginástica a fim de fortalecer seus corpos para que, mais tarde, com a alma suficientemente madura, sirvam a filosofia.

Uma vez formado o filósofo, como este conseguirá apoderar-se da administração do Estado? Como administrará o Estado? O processo no qual isso se dará é, em suma, o seguinte: (1) O filósofo, concentrado naquilo que é fixo e ordenado, torna-se ele mesmo ordenado, (2) O povo convencer-se-á de que os filósofos são os mais aptos para o Estado na medida em que lhes for apresentados os verdadeiros filósofos, (3) Uma vez em cargo público, o filósofo tentará não apenas modelar a si próprio, mas os costumes públicos também, limpando o caráter das pessoas e do Estado, não se limitando apenas a fazer leis, (4) Uma vez atingido tal objetivo, formulará um nova constituição, (5) Para aperfeiçoar essa constituição, o filósofo lançará mão de um processo sucessivo de abstrações e aplicações, ora de olho nas essências, ora de olho nos homens (c.f. Alegoria da Caverna).

Mas como, na atual e colapsada situação, tal plano poderá ser empreendido? Bastam dois elementos: (a) um filósofo, apenas um, e (b) uma cidade minimamente aberta a suas opiniões. É difícil, lembra Sócrates, mas não impossível.

* * *

Sócrates, a fim de mostrar a distância ou a diferença entre conhecimento e ignorância, lança mão da alegoria da caverna.

Alegoria => Realidade
===============

Caverna => Mundo que nos cerca
Sombras => Objetos visíveis
Fogo => Sol
Região superior => Mundo inteligível
Subida à região superior => Ascensão da alma
Muro -> Estrada -> Objetos -> Fogo -> Exterior => Diversas etapas da ascese
Prisioneiro que se liberta => Filósofo
Sol (fonte de toda luz) => Idéia do Bem (causa de tudo o que de reto e belo existe)
Olho do corpo => Olho da alma (intelecto)
Conversão (virar o olho para a luz, com todo o corpo) => Conversão (virar o intelecto para a luz, com toda a alma)

A caverna é, assim, o âmbito dos ignorantes, daqueles que tomam as sombras pelas coisas reais. Mas a alegoria não é útil apenas para mostrar a distância entre ignorância e conhecimento, mas também para mostrar que embora a ascensão ao bem seja a melhor das atitudes, uma vez lá, os filósofos devem descer para as sombras a fim de instruir os homens ignorantes, não importa se mereçam ou não tal instrução. Tal faz-se necessário porque o Estado interessa-se pela felicidade de todos, não apenas de uma classe de poucos.

* * *

SELF-TESTING QUESTIONS

1. Por que os enigmas de trocadilhos são como os objetos da opinião?

Porque os enigmas nem revelam nem escondem por completo aquilo a respeito de que versam. Analogamente, as opiniões, embora se refiram a coisas reais, não lidam com suas essências. Um sofista, um professor de opiniões, expressa-se a respeito da beleza da flor ou de uma estátua, mas não é capaz de expressar-se sobre a beleza em si, sobre a essência da beleza.

2. Que tipo de homem causa o maior dano à filosofia?

Os sofistas, os imitadores da filosofia, os professores de opiniões.

3. Quais os bens da vida comum que distraem o filósofo?

Beleza, riqueza, força, cargo, relações no Estado.

4. Quem é comparado ao “ferreiro baixo e calvo”, que tenta elevar-se acima de seu lugar?
Os sofistas, os imitadores da filosofia.

5. Quais as diversas condições que podem salvar um homem para a filosofia?

Aquelas que, de uma forma ou de outra, mantêm o filósofo distante das distrações e do ambiente antifilosófico: exílio, desprezo pela política, doença etc.

6. Que mudanças no ensino da filosofia Sócrates defende?

Enfatizar a educação física nas crianças e jovens e ensinar-lhes pouca filosofia, evitando temas complexos e desgastantes como a dialética.

7. A que se refere a metáfora da “circuncisão” na alegoria da caverna?

Aos cortes das más influências e dos maus temperamentos, desde a tenra infância, no processo educacional que levará o jovem à conversão (“retirada da caverna”).

Pensando sobre Deus

Segue um resumo de How To Think About God, de Mortimer J. Adler, em forma Q&A.

Qual o objetivo do autor?

O objetivo de Adler, não é extamente provar a existência de Deus, mas inferir a existência de Deus. A diferença entre provar e inferir consiste no grau de certeza que resulta do raciocínio. Provar a existência de Deus implicaria em um elevado grau de certeza, semelhante àquele que atingimos nas demonstrações matemáticas e geométricas. Este não é o caso, já que Adler prefere o termo “inferir”, que rende ao raciocínio um grau de certeza inferior, mas que ainda assim está além da dúvida razoável.

Ao contrário de Santo Tomás, Moisés Maimônides e Avicena, Adler não pretende lançar mão de artigos de fé ou de Escrituras Sagradas para empreender seu raciocínio. Às obras desses autores, Adler chama de teologia sacra. No entanto, mesmo Leibnitz, Descartes e demais autores que tentaram evitar se deixar influenciar pelas religiões ao pensar acerca de Deus – a chamada teologia natural – Adler crê que não obtiveram sucesso.

Adler apresenta sua obra como sendo pura teologia filosófica, completamente isenta de influências religiosas e artigos de fé.

A existência de Deus não pode ser provada simplesmente argumentando que o mundo precisa de um Criador?

Não.

As religiões ocidentais nos dizem que Deus criou o mundo. Mas tal é simplesmente um artigo de fé, sustentado por cristãos, judeus e muçulmanos. No entanto, um filósofo deve esquivar-se de aceitar esse artigo de fé como verdade comprovada.

A ciência, por outro lado, nada nos diz a respeito da criação do mundo. A teoria do Big Bang versa sobre a origem do mundo, mas do mundo que conhecemos. Isso significa que o Big Bang não explica a exniquilação do mundo, ou seja, a criação do mundo a partir do nada. ["Exniquilação" é um termo criado por Adler em contraposição a "aniquilação", ou seja, a redução de algo a nada]. A ciência não pode provar de que maneira aquela massa que explodiu foi criada, nem mesmo se havia o tempo antes dela.

A filosofia, portanto, tem duas alternativas: ou o mundo foi criado por uma agência criadora, ou o mundo sempre existiu e sempre existirá (posições assumidas por Santo Tomás e Kant, por exemplo). Como não devemos assumir justamente a opção que se deseja provar, devemos adotar a noção de que o mundo sempre existiu e sempre existirá, ou seja, o mundo tem uma existência perpétua.

E quanto à primeira causa? Não é necessário que o mundo tenha uma primeira causa que explique sua existência?

Não.

Se dissermos que, temporalmente, é necessário haver uma primeira causa não-causada que tenha colocado em marcha o movimento e a mudança do mundo, assumiríamos implicitamente que o tempo é limitado. Incorreríamos no erro anterior.

Se, por outro lado, argumentarmos que a primeira causa é superior, ou seja, está acima dos fenômenos naturais, sendo estes intrumentos na mão daquela, e não temporalmente anterior, também incorreríamos em erro. Não há no mundo natural nada que nos obrigue a considerá-lo como instrumental. Nada nele nos diz, além das próprias ciências naturais, que há um causador (ou hierarquia de causas) por detrás dele.

Como definimos "Deus"?

Para iniciarmos nossa inferência da existência de Deus, temos primeiramente de tentar definir a palavra “Deus”. Ao contrário das palavras “lápis”, “justiça” etc., que são nomes comuns, ou seja, comuns a mais de um objeto individual, “Deus” é um nome próprio, como “Edward H. Wolff” ou “Mortimer J. Adler”. Ora, sabemos que para as pessoas usarem os nomes próprios enquanto tais, devem:

(1) ser apresentadas pessoalmente ao indivíduo que leva o nome.
(2) devem ser indicadas ao indivíduo que leva esse nome.
(3) devem ser apresentadas a uma descrição que identifique o indivíduo que leva esse nome.

Ocorre que “Deus” não é alguém a quem possamos ser apresentados ou a quem possamos apontar. Mesmo no caso de Abraão, Moisés, Jesus Cristo etc., cujo conhecimento de Deus foi direto, tal conhecimento exige de nós uma fé religiosa anterior para acreditarmos.

Vemos então que “Deus” é inclassificável, não sendo, strictu sensu, um nome próprio. Não somos capazes de conhecê-lo ou apontá-lo, então precisamos de uma descrição definitória, isto é, que defina Deus.

Por que não podemos definir “Deus”?

Porque Deus, sendo um nome próprio, não é passível de ser definido, tanto quanto “Edward H. Wolff” não é passível de definição. Uma definição aplica-se a uma classe ou grupo de objetos. Um nome próprio não é uma classe de objetos, mas um indivíduo singular. Deus, portanto, deve ser descrito, não definido. Essa descrição tem de possuir um caráter identificatório, ou seja, essa descrição deve chegar ao ponto de podermos identificar Ele, e somente Ele, como objeto da descrição.

Um nome próprio é pode ser descrito de várias maneiras, encaixando-o em diversas classes. Edward H. Wolff é brasileiro, engenheiro, que nasceu em 1976, na cidade de São Paulo etc. Mas Deus é inclassificável, isto é, não é passível de ser classificado com palavras que possam ser compartilhadas com outros indivíduos. Quando uma palavra designa uma característica comum a dois objetos, essa palavra tem de ser aplicada exatamente no mesmo sentido a ambos, ou seja, ao descrevermos Deus, temos de evitar usar classes aplicáveis a outros objetos.

Adler lança um alerta contra os discípulos de Kant, que acham que a razão não deve lidar com objetos além da experiência sensorial, como é o caso de Deus. Ora, basta a ciência moderna, que lida com buracos negros, prótons, inconsciência etc., conceitos esses que a lógica moderna chama de constructos teóricos em contraposição aos conceitos empíricos, para dispensar qualquer espistemologia kantiana de nossa parte.

Como formular uma descrição de Deus?

O primeiro passo que Adler adota para formular uma descrição de Deus é lançar mão do chamado “argumento ontológico”, de Anselmo. Esse argumento nos ajudará a compor a descrição, embora Adler insista em lembrar-nos que não considera o argumento ontológico como válido como prova da existência de Deus.

Segundo Anselmo, (1) se pensarmos num ser cuja grandeza maior não há (isto é, o ser supremo), segue-se que (2) este ser tem de necessariamente existir pois, de outra forma, não seria o ser supremo, mas algo inferior a ele, além de (3) não poder não existir, ou seja, sempre existiu e sempre existirá.

O segundo passo que Adler adota para formular uma descrição de Deus é investigar a seguinte questão: “Se Deus reamente existisse, como seria a existência dele?”

Há três respostas possíveis: (a) Deus é totalmente diferente das outras coisas, (b) Deus é totalmente semelhante às outras coisas e (c) Deus é tanto diferente quanto semelhante às outras coisas.

A primeira resposta é incompatível com a pergunta porque há uma suposição, que consta na própria pergunta, que diz: “Se Deus realmente existisse”. Ora, se Deus fosse totalmente diferente de tudo, então não teria real existência.

A segunda resposta insinua que Deus é corpóreo, material, físico. Mas como Deus não pode ser parte do cosmos (senão Deus não seria supremo), nem o cosmos parte de Deus (senão o cosmos não seria a totalidade do mundo), nem o cosmos igual a Deus (senão o cosmos seria a coisa cuja grandeza maior não haveria), temos de descartá-la.

A terceira resposta, portanto, é a única resposta possível: Deus é diferente de tudo por ser imaterial e semelhante a tudo na medida que sua existência real e a existência real do mundo é analógica, não-unívoca, ou seja, Deus e as coisas do mundo existem enquanto objetos de pensamento, mas diferenciados entre aquilo que é corpóreo e incorpóreo, material e imaterial, físico e espiritual, natural e supernatural.

Em resumo, o objeto de pensamento “Deus” possui as seguintes notas descritivas:

(1) é o ser supremo
(2) possui existência real no sentido analógico do termo
(3) é imaterial, incorpóreo, não-físico
(4) é supernatural (conseqüência de ser imaterial)
(5) infinito, pois Deus não é um exemplar individual de uma classe de coisas cuja existência é finita
(6) eterno, pois a existência de Deus é necessária, e não contingente, como as coisas do mundo que nascem/morrem. Por ser necessária sua existência, Deus é independente, incondicionado, incausado e, acima de tudo, possui “aseidade” (do latim a se, isto é, existência em, através e de si mesmo.

Como inferimos a existência de Deus?

Antes de versarmos sobre a existência de Deus, versemos sobre como inferir a existência de qualquer coisa. As inferências existenciais dividem-se em dois tipos:

(a) inferências a respeito da existência real de uma entidade singular única; por exemplo: “os avós do meu amigo existem”.
(b) inferências a respeito da existência real de entidades singulares de uma dada classe de entidades; por exemplo: “elétrons existem”.

Quanto ao 1º tipo, só podemos confirmar a dada inferência por meio do contato direto perceptual. O Abominável Homem das Neves, por exemplo, pode ter sua existência inferida por alguém que o viu pessoalmente ou por alguma evidência perceptual (as pegadas na neve do Himalaia).

Quanto ao 2 º tipo, sua inferência só pode ser feita caso a existência de tais entidades seja necessária para a explicação de certo fenômeno. É a famosa regra de William of Ockham. A navalha de Ockham elimina as hipóteses cuja existência é dispensável. Os constructos teóricos que se salvam da navalha permanecem, no entanto, apenas hipóteses.

Para ambos os tipo, as inferências não podem ser chamadas de “provas”, como a força de uma prova matemática ou geométrica. Assim como num tribunal, os vereditos baseiam-se na preponderância das evidências ou além da dúvida razoável, mas ainda estão num grau abaixo da prova.

No caso da existência de Deus, por ser Deus inclassificável, sua inferência é uma mistura das características dos dois grupos, tornando-a única e singular. Ao contrário dos buracos negros ou dos elétrons, a existência de Deus não é inferida por experimentos ou observações, mas pela existência de entidades individuais ou do cosmos como um todo. No caso do elétron, o constructo teórico e derivado de observações. No caso de Deus, o constructo teórico é justamente o ponto de partida. No caso do elétron, qualquer observação incongruente pode invalidar o constructo teórico. No caso de Deus, isso não é possível.

Adler lembra ainda que o argumento ontológico de Anselmo falha porque implica em assumir a existencia de Deus como auto-evidente. Ocorre que as proposições existenciais nunca são auto-evidentes, isto é, nunca são necessariamente verdadeiras, cujo oposto é impossível. O fato de termos uma noção daquele objeto de pensamento em mente não o torna automaticamente verdadeira, mesmo que na descrição dessa noção esteja incluída a nota de que tal existência seja necessária. Adler acredita ter driblado o argumento ontológico ao propor se Deus existisse, como ele seria. Tudo não passou de uma hipótese.

Chegamos ao ponto de apresentarmos o chamado “argumento cosmológico” para a existência de Deus. Adler considera o melhor argumento, mas não livre de falhas. Para explicá-lo, é necessário antes explicarmos três termos utilizados pelo argumento cosmológico:

(a) Ser contingente. É aquele cuja existência depende da existência de outro ser. Em outras palavras, é um ser cuja existência se dá em, para e por meio de outro ser. Em latim, diz-se que sua existência é ab alio.

(b) Ser necessário. É aquele cuja existência não é causada, é independente. Em latim, diz-se que sua existência é a se.

(c) Causa do ser (causa essendi). É a causa que não explica somente o movimento/alteração/geração das coisas. Essas seriam causa fieri, como a bola de bilhar empurrada pelo taco ou o filho gerado pelos pais. Uma vez que as causa fieri cessam de atuar, a existência dos efeitos não cessa. Uma bola de bilhar não deixa de existir porque o taco cessou de empurrá-la. Similarmente, não foi o taco o responsável por sua existência. Portanto, a causa essendi deve explicar tanto a existência do ser quanto sua causa eficiente. Por exemplo, o oxigênio não é a causa essendi do fogo porque não foi ele o responsável por sua causa eficiente, mas sim o fósforo.

A partir do entendimento dos três termos acima, podemos adotar 5 premissas:

(1) A existência de um efeito implica a existência de sua causa.
(2) Aquilo que existe ou precisa ou não precisa de uma causa essendi.
(3) Um ser contingente é aquele que precisa de uma causa para sua existência a cada instante que dure sua existência, caso contrário é reduzido a aniquilação.
(4) Nenhum ser contingente é capaz de causar a existência de outro ser contingente, mas apenas ser a causa fieri de outro ser contingente.
(5) Os seres contingentes existem neste mundo e continuam a existir desde sua geração até seu perecimento.

Então, o argumento (ou inferência) cosmológico conclui que um ser necessário é a causa que age para sustentar a existência de seres contingentes. Ou seja, em suma, dado que seres contingentes existem, então Deus existe.

Por que este argumento cosmológico é falho?

Por causa de duas falhas presentes na premissa (3):

(a) Não é verdade que uma causa é necessária para explicar a existência de um ser. Adler usa o exemplo da lei da inércia. Uma vez que o taco atinge a bola e a coloca em movimento, essa bola continuaria a se mover não fosse a existência de causas eficientes contrárias ao movimento (atrito etc). Caso contrário, a bola moveria-se indefinidamente, sem uma causa que lhe imprima o efeito. Similarmente, as coisas naturais, uma vez geradas, também existiriam perpetuamente não fossem outras causas naturais que as fizessem perecer.

(b) Não há nada no mundo, nenhuma evidência, que nos mostre que coisas são aniquiladas ou exniquiladas. Quando algo perece, não há aniquilação mas transformação de uma coisa em outra. Isto significa que a contingência das coisas não é radical (ser/não ser), mas superficial (ser uma coisa/ser outra coisa).

Como corrigir o argumento cosmológico?

Adler acredita que o argumento acima não é verdadeiramente cosmológico porque não se fundamenta no cosmos como um todo.

Adler explica que a existência do cosmos tem de ser radical, isto é, não pode ser superficial. Ora, o cosmos, ou seja, a totalidade de todas as coisas, não pode transformar-se em outra coisa pois continuaria a ser o cosmos. Isso se explica pelo fato de o cosmos não ser como os outros seres individuais, cuja origem é a transformação de algo para perecer transformando-se em outro algo. Afinal, este algo teria sido o próprio cosmos. Similarmente, a totalidade de todas as coisas (cosmos) não perece transformando-se porque isso, para o cosmos, não seria um perecimento, mas simples continuação de sua existência enquanto totalidade de todas as coisas.

A partir desda compreensão, Adler estabelece as 4 premissas de seu argumento cosmológico:

(1) A existência de um efeito que requer a correspondente existência de uma causa implica na existência dessa causa.

(2) O cosmos como um todo existe.

(3) A existência do cosmos é radicalmente contingente, de maneira que, embora não precise de uma causa efeiciente que o tenha gerado (supondo o cosmos perpétuo no tempo passado), exige uma causa eficiente que o afaste da aniquilação.

(4) Dado que o cosmos precisa dessa causa eficiente que o sustente, tal causa não pode ser natural, mas sobrenatural, já que causas naturais não são capazes de aniquilar nada.

Por que o cosmos é contingente?

O cosmos é contingente porque ele é apenas um dentre muitos possíveis cosmos. É perfeitamente possível pensar num cosmos diferente, com leis naturais diferentes, com arranjos e ordens diferentes. Este cosmos em que vivemos é um numa pluralidade de cosmos possíveis. Se este cosmos é possível, isso significa que também é possível que o cosmos não exista, assim como qualquer coisa possível (isto é, não-necessária).

Ocorre que um cosmos meramente possível tem de ser um cosmos causado, caso contrário seria um cosmos necessário. O cosmos possível exige uma causa sobrenatural, um ser supremos, que sustente e preserve sua existência.

Deus é, nesta óptica, a causa preservativa do cosmos, uma vez que excluímos Deus de ser a causa criativa do cosmos em nossa premissa de um cosmos perpétuo. Se quiséssemos, poderíamos assumir Deus como a causa criadora do cosmos, já que a premissa adotada não por motivos racionais, mas por uma questão de gosto.

Vale notar que a ação preservativa de Deus é a ação preservativa de todos nós, dado que Deus preserva o cosmos da aniquilação, isto é, preserva todas as coisas da aniquilação.

Diante deste argumento, Adler afirma ter “bases razoáveis para afirmar a existência de Deus”.